What is a harmonic?
A harmonic of a particular frequency (the fundamental frequency F) is a frequency that is an integer multiple of the first one. For example:
if f = 125 MHz, the harmonics would be:
1st harmonic = 1f = 125 MHz
2nd harmonic = 2f = 250 MHz
3rd harmonic = 3f = 375 MHz
4th harmonic = 4f = 500 MHz
….. etc.
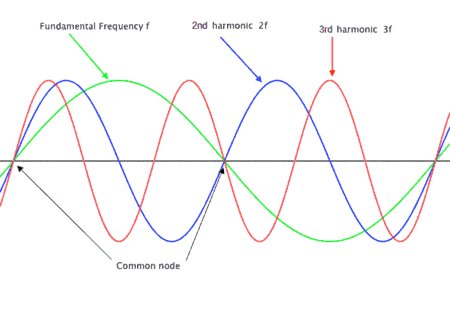
In the diagram below it can be seen that harmonics share common nodes.
Mathematically, the basic wave equation is:
<math> \mathit{v}=\mathit{f}\times \lambda </math>
v is the velocity of the wave in meters per second – a constant close to the speed of light for radio waves in the atmosphere.
f is the frequency of the wave – how many cycles pass a fixed point per second
<math> \lambda </math> is the wavelength of the wave in meters – the distance between two peaks of the wave.
So, as the frequency increases, the wavelength decreases – a doubling of frequency causes a halving of wavelength, etc.


simple but easy to understand